Truncating decimals from summands and sum

This is a problem that you may have run into at some point. Especially, if you had to display or print the components of a price using less decimals than the decimals used for the calculations.

Cutting-off decimals after the calculation has taken place can lead to inconsistency between the summands and the sum. In general, the sum of rounded numbers is not the same as their rounded sum. This happens when the sum of the lost decimals adds one or more units to a higher decimal place (that is not lost).

Let’s take the following calculation as an example:

Product 1     Product 2     Product 3      Product 4     Product 5   Total

  2,2342       1,7437        1,1247         1,5785       1,1233     7,8044

If we round all numbers, we will end up with this (with colors we illustrate the discrepancy from the original value):

Product 1     Product 2     Product 3      Product 4     Product 5   Total

  2,23         1,74          1,12           1,58         1,12       7,80

 -0,0042      -0,0037       -0,0047        +0,0015      -0,0033    -0,0044

---------------------------------------------------------------   -----------
                              - 0,0144                            - 0,0044

Something is off here. If you sum up the products, you get 7,79. Not 7,80 . It is even worse if you try to just truncate the decimals from the summands instead of rounding them (they will add up to 7,78).

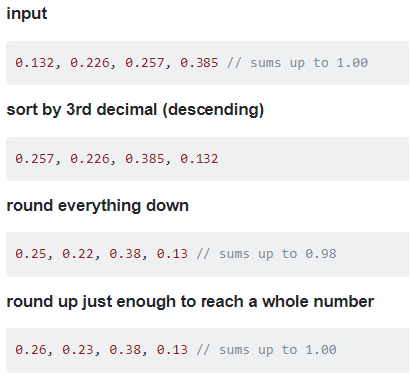
So, just rounding everything doesn’t work. However, there is a way to adjust the rounded values in order to keep the summation consistent. The technique is illustrated in the following image. It is is an example of cutting off the third decimal from a group of numbers that add up to one (e.g percentages):

Now, let’s write some code in PHP that implements this technique:

function trucateSummingFloat($numbers, $numberOfDecimalsToKeep)
    {
        $shiftNum      = pow(10, $numberOfDecimalsToKeep);
        $shiftNumPlus1 = pow(10, $numberOfDecimalsToKeep + 1);

        $originalSum      = array_sum($numbers);
        $origTruncatedSum = (round($originalSum * $shiftNum) / $shiftNum);
        $n                = count($numbers);

        // create metadata object for each number
        $metaNums = [];
        for ($i = 0; $i < $n; $i++) {
            $metaNums[] = [
                'index'        => $i,
                'thirdDecimal' => floor($numbers[$i] * $shiftNumPlus1) % 10,
                'prefix'       => floor($numbers[$i] * $shiftNum)
            ];
        }

        // Sort from highest third decimal to lowest
        usort($metaNums, function ($item1, $item2) {
            if ($item1['thirdDecimal'] == $item2['thirdDecimal']) {
                return 0;
            }

            return ($item1['thirdDecimal'] > $item2['thirdDecimal']) ? -1 : 1;
        });


        // Calculate integer-ed sum based on truncated summands
        $sum = 0;
        for ($j = 0; $j < $n; $j++) {
            $sum += $metaNums[$j]['prefix'];
        }

        // find number of units we are missing from the lowest decimal we will keep
        $numberOfIncrements = $origTruncatedSum * $shiftNum - ($sum);

        // add missing units to summands starting from ones with highest truncated part
        for ($k = 0; $k < $numberOfIncrements; $k++) {
            $metaNums[$k % $n]['prefix']++;
        }

        // sort the numbers back to input order
        usort($metaNums, function ($item1, $item2) {
            if ($item1['index'] == $item2['index']) {
                return 0;
            }

            return ($item1['index'] < $item2['index']) ? -1 : 1;
        });

        $truncatedFloats = [];
        for ($l = 0; $l < $n; $l++) {
            $truncatedFloats[] = $metaNums[$l]['prefix'] / $shiftNum;
        }

        return $truncatedFloats;
    }

And, now, let’s use this function:

$numbers = [2.2342, 1.7437, 1.1247, 1.5785, 1.1233];
        $originalSum      = floor(array_sum($numbers) * 100) / 100;
        $truncatedNumbers = trucateSummingFloat($numbers, 2);
        $finalSum         = array_sum($truncatedNumbers);

        print_r($numbers);
        print_r('Truncated sum of original numbers: ' . $originalSum);
        print_r($truncatedNumbers);
        print_r('Sum of truncated numbers: ' . $finalSum);